Essence of calculus is derivative, that is the instantaneous rate of change of a function with respect to one of its variables, which is equivalent to finding the slope of the tangent line to the function at a point (Watkins et al., 1999). Position, change of position, and various rates of change of position are referred as kinematic variables, where the terms kinematics means the study of motion, from the Greek word for movement, kinesis (Redish, 2019). If position is something as function of time, the first derivative gives its velocity, and the second derivative gives its acceleration, or simply differentiate position to get velocity and further differentiate velocity to get acceleration (Zegarelli, 2021), where the derivative means derivative with respect to time.
position and its derivatives Link to heading
Suppose that there is position as function of time t in 3-d
$$ \begin{array}{rcl} \vec{r} & = & x \ \hat{i} + y \ \hat{j} + z \ \hat{k} \newline & = & x \ \hat{e}_x + y \ \hat{e}_y + z \ \hat{e}_z \newline & = & x \ \hat{x} + y \ \hat{y} + z \ \hat{z} \newline & = & x_1 \ \hat{x}_1 + x_2 \ \hat{x}_2 + x_3 \ \hat{x}_3 \newline & = & x_1 \ \hat{e}_1 + x_2 \ \hat{e}_2 + x_3 \ \hat{e}_3, \end{array} $$
where the first style is common in high school, second and third styles in college of science, and the last two styles in college of engineering. It would be better that all styles is understood. Third style will be used here.
Velocity is first derivative of position with respect to time
$$ \begin{array}{rcl} \vec{v} & = & \displaystyle \frac{d\vec{r}}{dt} \newline &&\newline & = & \displaystyle \frac{dx}{dt} \ \hat{x} + \frac{dy}{dt} \ \hat{y} + \frac{dz}{dt} \ \hat{z} \newline &&\newline & = & v_x \ \hat{x} + v_y \ \hat{y} + v_z \ \hat{z} \newline \end{array} $$
and acceleration is first derivative of velocity
$$ \begin{array}{rcl} \vec{a} & = & \displaystyle \frac{d\vec{v}}{dt} \newline &&\newline & = & \displaystyle \frac{dv_x}{dt} \ \hat{x} + \frac{dv_y}{dt} \ \hat{y} + \frac{dv_z}{dt} \ \hat{z} \newline &&\newline & = & a_x \ \hat{x} + a_y \ \hat{y} + a_z \ \hat{z} \newline \end{array} $$
or second derivative of position.
The relation between position and its derivatives can also be displayed for each coordinate, e.g.
$$ v_x = \frac{dx}{dt}, \ \ \ \ a_x = \frac{dv_x}{dt}, $$
for $x$ coordinate,
$$ v_y = \frac{dy}{dt}, \ \ \ \ a_y = \frac{dv_y}{dt}, $$
for $y$ coordinate, and
$$ v_z = \frac{dz}{dt}, \ \ \ \ a_z = \frac{dv_z}{dt}, $$
for $z$ coordinate.
a numerical example Link to heading
A point mass particle has following position
$$ \vec{r} = [(10 + 3t) \ \hat{x} + (1 + 4t - 5t^2) \ \hat{y} + 50 \ \hat{z}] \ {\rm m}. $$
Then, its velocity is
$$ \vec{v} = [3 \ \hat{x} + (4 - 10t) \ \hat{y}] \ {\rm m/s}. $$
And also its acceleration is
$$ \vec{a} = -10 \ \hat{y} \ {\rm m/s^2} $$
Notice that differentiation can be performed directly to the vector or to each component, e.g. $x$, $y$, $z$, first and then combine the results back to form a vector.
graphs Link to heading
By taking only component in y direction following graphs can be drawn.
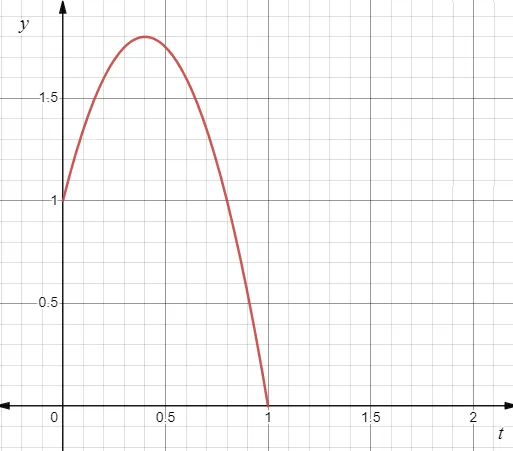
Above is position $y = (1 + 4t - 5t^2) \ {\rm m}$ with maximum point is located at (0.4, 1.8).
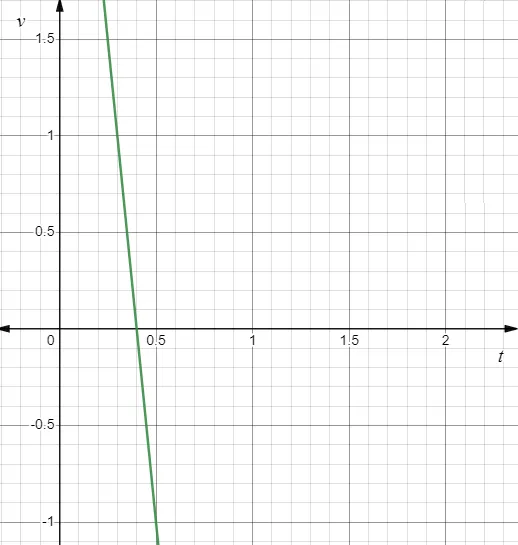
Velocity function is $v = (4 - 10t) \ {\rm m/s}$ with zero velocity is found at t = 0.4 s.
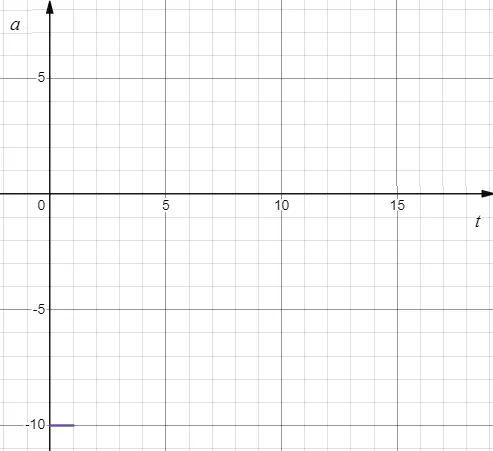
Then finally the acceleration is simply $a = -10 \ {\rm m/s^2}$, which remains constant all time.
Note: Previous three figures are created using Desmos.
challenges Link to heading
- Use component in $z$ direction and find velocity and acceleration. Draw also the graphs. Do it the same way for component in x direction.
- For the component in $y$ direction, what are the information relating maximum point and velocity? Explain in brief.
- Could two different functions of time for position lead to the same function of time for velocity? Explain the answer with three different examples.
- A particle is moving along $x$ direction with its position $x = e + bt + ct^2$. Find its velocity and acceleration as function of time. What is the relation of $e$, $b$, and $c$ if the particle once stops at time $t = t_1$?
- There are two particles with positions $x₁ = (10 + 2t)$ m and $x₂ = (2 + 4t)$ m. 6. Find velocity as function of time for both particles. Which particle is ahead the other at time $t = 0, 4, 8$ s? Does it depend on the velocity? Explain it.
- Suppose that a point mass particle has following position as function of time, $x = (2 + \cos 0.25π t)$ m dan y = (3 + \sin 0.25π t) m. Find its velocity and acceleration. Draw its trajectory accompanied by its velocity and acceleration at time t = 0, 1, 2, 3, 4, 5, 6, 7 s.
- In calculate the derivative of position, why the derivative of unit vectors are not taken into account? Does it hold only for Cartesian coordinate system or also in other coordinate system as polar coordinate system?
Read this on Medium @6unpnp/d335de4e1676