Relative position of an object is position of the object measured relatively from other object, which simply substraction of the object position and other object position (Smith, 2012). Numerical calculation in solving physics problem is recommended, because the difficulty faced by the students will be a valuable experience in advancing their understanding and skill (Allain, 2017). Here illustration about relative position is given and it is also accompanied with a numerical example.
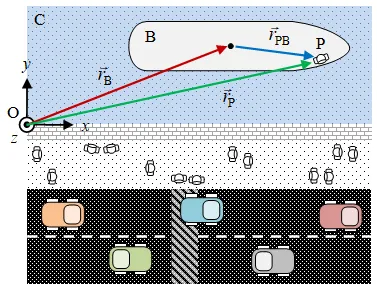
Figure 1. A passanger P is on boat B, which is moving along a canal C.
Suppose that there is a moving boat B along a canal C, where on the boat there is a passanger P walk on the boat.
notation Link to heading
As the illustration example in Figure 1 will be used, where there are passanger on a moving boat along a canal. Point O, a point on an edge of the canal, can be considered as fixed point in rest reference of frame. Position of the boat B can be defined relatively to this point as
$$ \vec{r} _{\rm BO} = \vec{r} _{\rm B} - \vec{r} _{\rm O}, $$
where rB and rO are vector in global frame of reference. Similar to previous equation relative position of passanger P to the boat B is simply
$$ \vec{r} _{\rm PB} = \vec{r} _{\rm P} - \vec{r} _{\rm B}. $$
Then, position of passanger P relatively to the canal will be
$$ \vec{r} _{\rm PO} = \vec{r} _{\rm P} - \vec{r} _{\rm O}, $$
Notice that relative position with indices A folowed by B means vector position of A minus vector position of B, and position vector with only one letter index can be considered that second index is simply (0, 0, 0).
numerical calculation Link to heading
In order to get quantitative sense of previous example, Figure 1 is detailed as follow.
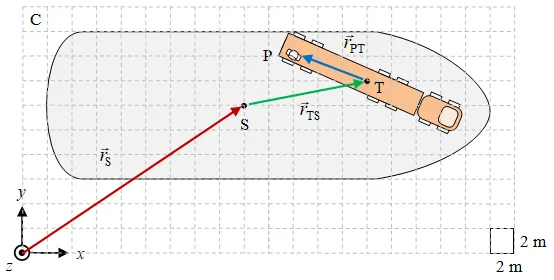
To provide quantitative value Figure 2 is drawn with grid size of 2 m × 2 m. Then following relative position can be obtained
$$ \begin{array}{rcl} \vec{r} _{\rm S} & = & (9 \cdot 2) \hat{x} + (6 \cdot 2) \hat{y} = 18\hat{x} + 12\hat{y}, \newline \vec{r} _{\rm TS} & = & (5 \cdot 2) \hat{x} + (1 \cdot 2) \hat{y} = 10\hat{x} + 2\hat{y}, \newline \vec{r} _{\rm PT} & = & (-3 \cdot 2) \hat{x} + (1 \cdot 2) \hat{y} = -6\hat{x} + 2\hat{y}. \end{array} $$
Besides above equation, there is also a relation
$$ \vec{r} _{\rm P} = \vec{r} _{\rm PT} + \vec{r} _{\rm TS} + \vec{r} _{\rm S}, $$
that, when it is substituted with previous equations, will produce
$$ \begin{array}{rcl} \vec{r} _{\rm P} & = & \vec{r} _{\rm PT} + \vec{r} _{\rm TS} + \vec{r} _{\rm S} \newline & = & d (-6\hat{x} + 2\hat{y}) + (10\hat{x} + 2\hat{y}) + (18\hat{x} + 12\hat{y}) \newline & = & (-6 + 10 + 18)\hat{x} + (2 + 2 + 12)\hat{y} \newline & = & 22\hat{x} + 16\hat{y}, \end{array} $$
that the result can be confirmed by calculating number of grids for $\vec{r}_{\rm P}$ from Figure 2.
challenges Link to heading
- What would be the result of $\vec{r} _{\rm PB} + \vec{r} _{\rm BO}$? Can you deduce something about index relation between relative position vectors?
- Using Figure 2 find $\vec{r} _{\rm T}$ directly by counting number of grids involved and by using $\vec{r} _{\rm S}$ and $\vec{r} _{\rm TS}$. Compare the two results and discuss it.
- A ship S is moving in x+ direction with velocity $v_{x}$ = 4 m/s. Write position of ship S as function of time t when its position at t = 0 s is as given in Figure 2.
Read this on Medium @6unpnp/136059d37e06