electromagnetic waves

Gelombang elektromagnetik (EM) merupakan salah satu jenis gelombang yang dirambatkan oleh variasi periodik simultan intensitas medan listrik dan magnetik dan yang termasuk dalam jenis gelombang ini adalah gelombang radio, cahaya inframerah, cahaya tampak, cahaya ultraviolet, sinar-x, dan sinar gamma [1]. Gelombang EM membawa energi, momentum, dan momentum angular menjauh dari partikel sumbernya dan dapat memberikan kuantitas-kuantitas tersebut pada bahan yang dilewatinya [2]. Sumber gelombang EM adalah partikel bermuatan yang dipercepat, partikel bermuatan menghasilkan medan listrik dan partikel bermuatan yang bergerak menghasilkan medan magnetik [3]. Persamaan gelombang yang muncul dari persamaan-persamaan Maxwell mendeskripsikan gelombang EM [4].

em spectrum#

Spektrum gelombang EM diklasifikasikan dengan panjang gelombangnya menjadi gelombang radio, gelombang mikro, cahaya inframerah, cahaya tampak, cahaya ultarungu, sinar-x, dan sinar gamma, dengan ilustrasinya diberikan pada gambar berikut ini.

Gambar 1. Spektrum gelombang elektromagnetik [5].

Mata manusia dapat mencerah gelombang EM dalam rentang cahaya tampak, yang pada Gambar 1 berada pada panjang gelombang sekitar 380 nm sampai 750 nm. Cahaya dengan panjang gelombang lebih pendek atau frekuensi lebih tinggi dari cahaya tampak disebut sebagai cahaya ultarungu, sedangkan cahaya dengan panjang gelombang lebih panjang atau frekuensi lebih rendah dari cahaya tampak disebut sebagai cahaya inframerah. Kata ultra (teramat sangat, lebih) dan infra (bawah, di bawah) pada gelombang terkait dengan frekuensi. Cahaya ultraungu berarti cahaya dengan frekuensi lebih tinggi dari cahaya ungu, sedangkan cahaya inframerah berarti cahaya dengan frekuensi lebih rendah dari cahaya merah.

wave equation#

Terdapat hubungan yang disebut sebagai persamaan gelombang [6, 7]

\begin{equation}\label{eqn:wave-equation} v = f \lambda \end{equation}

dengan $v$ laju rambat gelombang, $f$ frekuensi, dan $\lambda$ panjang geombang. Persamaan \eqref{eqn:wave-equation} berbeda dengan persamaan diferensial yang juga disebut sebagai persamaan gelombang [8, 9, 10, 11].

traveling wave#

Gelombang EM merupakan contoh dari gelombang merambat, yang dalam hal ini merambatkan energi dan juga fasanya, sehingga pada setiap titik dalam arah rambat gelombang fasanya selalu selalu berbeda dengan sumbernya, kecuali jaraknya tepat kelipatan bulat dari panjang gelombangnya [12].

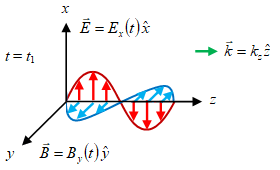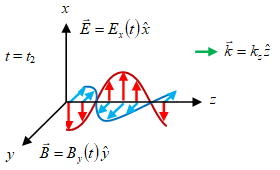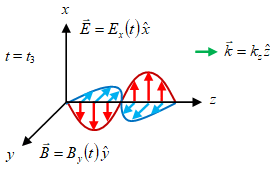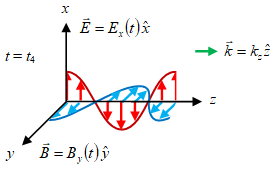Gambar 2. Gelombang EM merambat ke arah $z+$.

Animasi gelombang EM yang merambat ke arah $z+$ diberikan pada Gambar 1, dengan medan listrik $\vec{E}$ hanya berosilasi pada arah $x$ dan medan magnetik $\vec{B}$ yang berosilasi pada arah $y$. Vector $\vec{k}$ untuk muatan yang bergerak dalam medan EM disebut sebagai drift [13], akan tetapi pada Gambar 2 hanya menggambarkan arah perambatan gelombang EM dan tidak terkait dengan bilangan gelombang $k$.

Fungsi waktu dari kedua medan tersebut adalah

\begin{equation}\label{eqn:em-wave-traveling-to-z-e-field} \vec{E} = \hat{x} E_x \sin(kz - \omega t + \phi) \end{equation}

dan

\begin{equation}\label{eqn:em-wave-traveling-to-z-b-field} \vec{B} = \hat{y} B_y \sin(kz - \omega t + \phi). \end{equation}

Bentuk fungsi paling sederhana dari fungsi waktu kedua medan pada Persamaan \eqref{eqn:em-wave-traveling-to-z-e-field} dan \eqref{eqn:em-wave-traveling-to-z-b-field} adalah bentuk $\sin$ atau $\cos$.

propagation direction#

Arah rambat gelombang EM ditentukan dari perkalian silang medan listrik $\vec{E}$ dengan medan magnetiknya $\vec{B}$, yang dapat digunakan lambang $\hat{k}$ sebagai vektor yang menunjukkan arah perambatan gelombang EM [14]. Arah $\hat{k}$ ini dapat diperoleh dengan

\begin{equation}\label{eqn:em-wave-traveling-k} \hat{k} = \frac{(\vec{E} \times \vec{B})}{|\vec{E} \times \vec{B}|}. \end{equation}

Untuk melihat kaitan antara kedua medan EM dengan arah rambat gelombangnya seperti yang diberikan oleh Persamaan \eqref{eqn:em-wave-traveling-k} diberikan tiga gambar berikut ini.

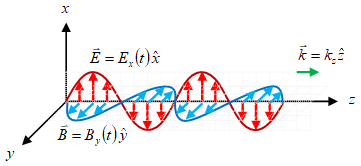Gambar 3. Gelombang EM merambat ke arah $z+$.

Penerapan Persamaan \eqref{eqn:em-wave-traveling-k} sebagai berikut

\begin{equation}\label{eqn:em-wave-traveling-to-z-k} \hat{k} = \frac{(E_x \ \hat{x} \times \hat{y} \ B_y)}{|E_x \ \hat{x} \times \hat{y} \ B_y|} = \frac{E_x \ B_y}{|E_x \ B_y|} \hat{z} \end{equation}

akan menghasilkan arah rambat seperti pada Gambar 3, yang dapat dipahami cukup dengan melihat pembilang pada ruas tengah Persamaan \eqref{eqn:em-wave-traveling-to-z-k} karena penyebutnya yang merupakan besar suatu vektor merupakan bilangan positif. Hasil akhirnya diperoleh pada ruas kanan.

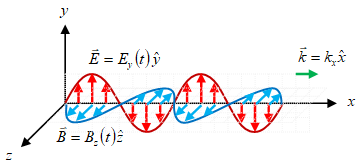Gambar 4. Gelombang EM merambat ke arah $x+$.

Selanjutnya adalah penerapan kembali Persamaan \eqref{eqn:em-wave-traveling-k} sebagai berikut

\begin{equation}\label{eqn:em-wave-traveling-to-x-k} \hat{k} = \frac{(E_y \ \hat{y} \times \hat{z} \ B_z)}{|E_y \ \hat{y} \times \hat{z} \ B_z|} = \frac{E_y \ B_z}{|E_y \ B_z|} \hat{x} \end{equation}

akan menghasilkan arah rambat seperti pada Gambar 4, yang dapat dipahami cukup dengan melihat pembilang pada ruas tengah Persamaan \eqref{eqn:em-wave-traveling-to-x-k} karena penyebutnya yang merupakan besar suatu vektor merupakan bilangan positif. Hasil akhirnya diperoleh pada ruas kanan.

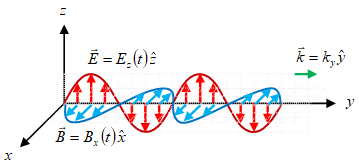Gambar 5. Gelombang EM merambat ke arah $y+$.

Dam penerapan kembali Persamaan \eqref{eqn:em-wave-traveling-k} sebagai berikut

\begin{equation}\label{eqn:em-wave-traveling-to-y-k} \hat{k} = \frac{(E_z \ \hat{z} \times \hat{x} \ B_x)}{|E_z \ \hat{z} \times \hat{x} \ B_x|} = \frac{E_z \ B_x}{|E_z \ B_x|} \hat{y} \end{equation}

akan menghasilkan arah rambat seperti pada Gambar 5, yang dapat dipahami cukup dengan melihat pembilang pada ruas tengah Persamaan \eqref{eqn:em-wave-traveling-to-y-k} karena penyebutnya yang merupakan besar suatu vektor merupakan bilangan positif. Hasil akhirnya diperoleh pada ruas kanan.

energy#

Gelombang EM membawa energi saat merambat melewati ruang kosong. Laju energi yang dirambatkan per satuan luas dideskripsikan dengan vektor Poynting

\begin{equation}\label{eqn:poynting-vector} \vec{S} = \frac{1}{\mu_0} \vec{E} \times \vec{B} \end{equation}

dan dikarenakan $\vec{E} \perp \vec{B}$ maka Persamaan \eqref{eqn:poynting-vector} akan menjadi

\begin{equation}\label{eqn:poynting-vector-magnitude} S = \frac{1}{\mu_0} EB. \end{equation}

Rata-rata laju energi per satuan luas yang dirambakan gelombang EM adalah

\begin{equation}\label{eqn:poynting-vector-magnitude-average} S_{\rm avg} = \frac{1}{2\mu_0} EB = \frac{1}{2c\mu_0} E^2, \end{equation}

dengan $c$ adalah laju rambat cahaya dalam vakum. Nilai rata-rata ini diperoleh dengan melakukan substitusi Persamaan \eqref{eqn:em-wave-traveling-to-z-e-field} dan \eqref{eqn:em-wave-traveling-to-z-b-field} ke Persamaan \eqref{eqn:poynting-vector-magnitude} dan dicari rata-ratanya dengan

\begin{equation}\label{eqn:poynting-vector-magnitude-average-calculation} S_{\rm avg} = \frac{1}{T} \int_t^{t + T} S \ dt, \end{equation}

seperti saat mencari daya rata-rata pada rangkaian AC atau nilai RMS untuk arus dan tegangan, akan tetapi sebelum langkah terakhir sehingga tidak perlu dicari nilai akarnya.

Selain itu terdapat pula besaran yang mengambarkan energi per satuan volume atau rapat energi yang dimiliki oleh suatu medan listrik

\begin{equation}\label{eqn:energy-density-e-field} u_E = \frac12 \epsilon_0 E^2 \end{equation}

dan medang magnetik

\begin{equation}\label{eqn:energy-density-b-field} u_B = \frac12 \epsilon_0 \frac{B^2}{\mu_0}, \end{equation}

di kedua persamaan terakhir terkait melalui

\begin{equation}\label{eqn:e=cb} E = cB. \end{equation}

electric field vector#

Gelombang EM, untuk saat ini, dapat dibahas cukup dengan hanya melihat medan listriknya, yang dengan ini telah dapat menjelaskan misalnya peristiwa polarisasi [15].

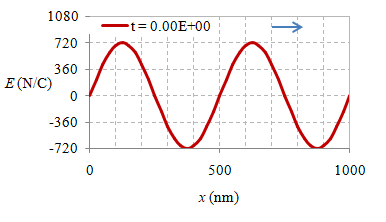
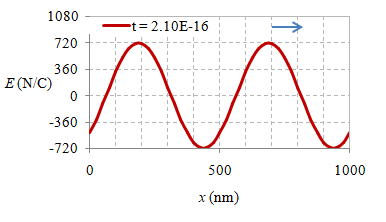
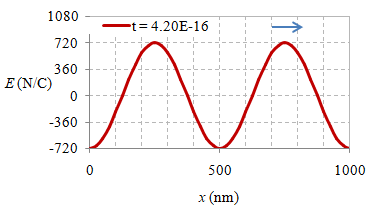
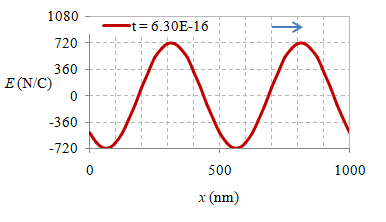
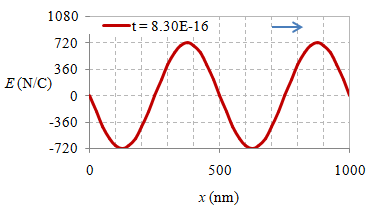
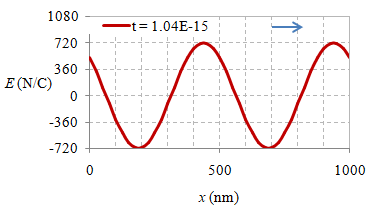
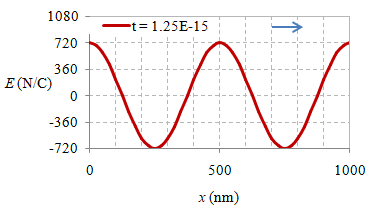
Beberapa foto suatu besaran fisis, yang dalam hal ini adalah medan listrik, pada delapan waktu berbeda $t$, $t + \frac18T$, $\dots$, $t + \frac12T$ $\dots$, $t + \frac34T$, $t + \frac78T$ diberikan di bawah ini.
 

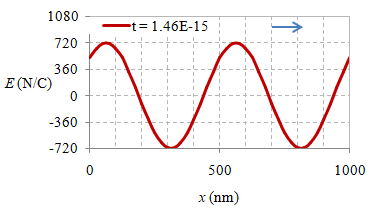Gambar 6. Rekaman medan listrik secara spasial pada waktu $t = 0 \ {\rm s}$, $2.10 \times 10^{-16} \ {\rm s}$, $4.20 \times 10^{-16} \ {\rm s}$, $6.30 \times 10^{-16} \ {\rm s}$, $8.30 \times 10^{-16} \ {\rm s}$, $1.04 \times 10^{-15} \ {\rm s}$, $1.25 \times 10^{-15} \ {\rm s}$, dan $1.46 \times 10^{-15} \ {\rm s}$.

Suatu gelombang EM yang merambat dalam vakum dapat direkam simpangan medan listriknya dalam rentang jarak $1000 \ {\rm nm}$ pada beberapa waktunya seperti diberikan pada Gambar 6, sedangkan animasinya diberikan pada gambar berikut ini.

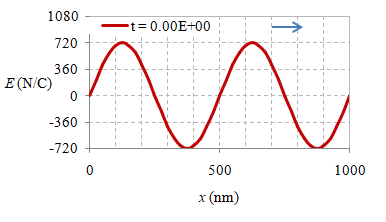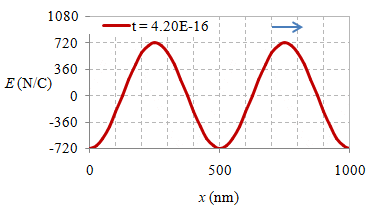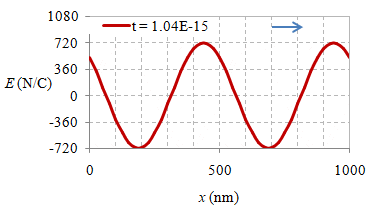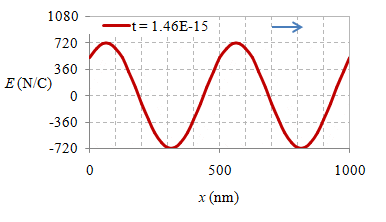Gambar 7. Gelombang EM merambat ke arah $x+$ dan terekam selama $1.67 \times 10^{-15} \ {\rm s}$.

Dari informasi pada Gambar 6 dan 7 dapat diperoleh panjang gelombang $\lambda$, periode $T$, fekensi $f$, dan amplitudo medan listrik $E_m$ dari gelombang EM tersebut.

exer#

  1. Tentukanlah $k_z$ pada pada Gambar 3 menggunakan Persamaan \eqref{eqn:em-wave-traveling-to-z-k}.
  2. Tentukanlah $k_x$ pada pada Gambar 4 menggunakan Persamaan \eqref{eqn:em-wave-traveling-to-x-k}.
  3. Tentukanlah $k_y$ pada pada Gambar 5 menggunakan Persamaan \eqref{eqn:em-wave-traveling-to-y-k}.
  4. Apakah satuan dari vektor Poynting pada Persamaan \eqref{eqn:poynting-vector}?
  5. Apakah satuan dari rapat energi pada Persamaan \eqref{eqn:energy-density-e-field} dan \eqref{eqn:energy-density-b-field}?
  6. Tentukanlah panjang gelombang $\lambda$, periode $T$, fekensi $f$, dan amplitudo medan listrik $E_m$ dari gelombang EM pada Gambar 6 dan 7.

notes#

  1. “electromagnetic wave”, Merriam-Webster, Inc., 2022, url https://www.merriam-webster.com/dictionary/electromagnetic%20wave [20220320].
  2. Wikipedia contributors, “Electromagnetic radiation”, Wikipedia, The Free Encyclopedia, 9 March 2022, 09:53 UTC, url https://en.wikipedia.org/w/index.php?oldid=1076096692 [20220320].
  3. Admin, “Electromagnetic Waves”, BYJU’S, 28 Apr 2021, url https://byjus.com/physics/electromagnetic-waves/ [20220320].
  4. Carl Rod Nave, “Electromagnetic Waves”, HyperPhysics, 2017, url http://hyperphysics.phy-astr.gsu.edu/hbase/Waves/emwavecon.html [20220320].
  5. Gringer Philip Ronan, “Revised diagram with re-aligned spectrum”, Wikimedia Commons, 19 Feb 2013, url https://commons.wikimedia.org/wiki/File:EM_spectrumrevised.png [20220321].
  6. Tom Henderson, “The Wave Equation”, The Physics Classroom, 2022, url https://www.physicsclassroom.com/class/waves/Lesson-2/The-Wave-Equation [20220321].
  7. Boundless.com, “https://courses.lumenlearning.com/boundless-physics/chapter/waves/", Boundless Physics, Lumen Learning, url https://courses.lumenlearning.com/boundless-physics/chapter/waves/ [20220321].
  8. OpenStax, “Mathematics of Waves”, Physics LibreTexts, OpenStax CNX, 8 Mar 2022, url https://phys.libretexts.org/@go/page/4070 [20220321].
  9. T. R. Akylas, C. C. Mei, “One-Dimensional Propagation”, I-campus project, School-wide Program on Fluid Mechanics, Modules on Waves in fluids, 9 Jul 2001, url http://web.mit.edu/fluids-modules/waves/www/material/chap-2.pdf [20220321].
  10. Jim Wheeler, “Solutions to the wave equation”, PHYS 3750 - Foundations of Wave Phenomena, Utah State University, 16 Sep 2019, url http://www.physics.usu.edu/Wheeler/Waves/WaveSolutions.pdf [20220321].
  11. Joel Feldman, “Solution of the Wave Equation by Separation of Variables”, Mathematics 267, Section 203, Mathematical Methods for Electrical and Computer Engineering, Department of Mathematics, University of British Columbia, 21 Jan 2007, url https://personal.math.ubc.ca/~feldman/m267/separation.pdf [20220321].
  12. Team, “what is the difference between travelling wave and stationary wave?” Topper Learning, 19 Mar 2011, url https://www.topperlearning.com/answer/what-is-the-difference-between-travelling-wave-and-stationary-wave/5evntguu [20220321].
  13. Christian Hill, “ExB drift for constant crossed electric and magnetic fields”, Learning Scientific Programming with Python, 17 Dec 2018, url https://scipython.com/blog/exb-drift-for-constant-crossed-electric-and-magnetic-fields/ [20220321].
  14. Di sini vektor satuan pada sistem koordinat digunakan $\hat{x}$, $\hat{y}$, dan $\hat{z}$ sehingga dapat digunakan $\hat{k}$ sebagai vektor satuan pada arah rambat gelombang EM.
  15. Marianne Breinig, “Electromagnetic waves”, Physics 421, Modern Optics, The University of Tennessee, Department of Physics and Astronomy, Spring 2015, url http://electron9.phys.utk.edu/optics421/modules/m1/emwaves.htm [20220321].